Distribución de probabilidad en el área de la salud

La distribución de probabilidad es una función que asigna a cada suceso definido sobre la variable aleatoria, la probabilidad de que dicho suceso ocurra. En el área de la salud este procedimiento matemático es de alta utilidad ya que permite representar en números e interpretaciones matemáticas hallazgos realizados en estudios previos conociendo la probabilidad de que ocurran ciertas variables. 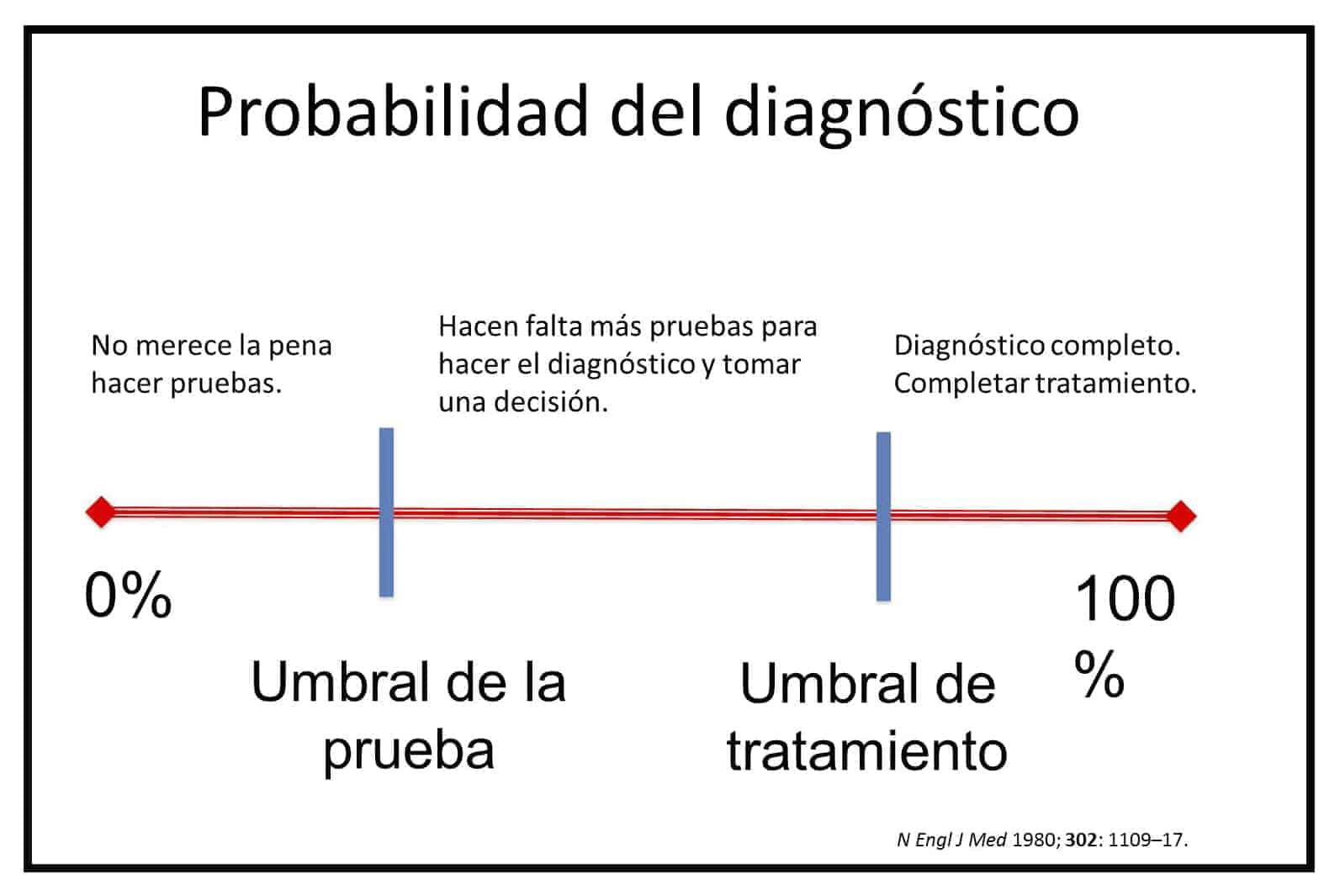Además de intervenir en estudios esto puede ayudar a la toma de decisiones pues demuestra la probabilidad y puede influir en la precisión del diagnóstico de un medicamento o en un tratamiento. También sirve para conocer la posibilidad de que una enfermedad ocurra o vuelva a aparecer, por ejemplo el dengue. Los resultados obtenidos en este proceso matemático pueden ser de utilidad para la prevención de la aparición de enfermedades o la repetición de las mismas.

Ejemplo:

Se realiza un estudio en el departamento de ginecología del Hospital universitario de los andes con el fin de conocer la edad con mayor incidencia de embarazos ectópicos en mujeres con edades comprendidas entre 20 a 23 años en una muestra de 8 mujeres.

14-20años = 1 mujeres

21-27 años = 3 mujeres

28-33 años = 3 mujeres

34-40 años= 1 mujeres

            Tabla 1. Distribución de probabilidad de embarazos ectopicos de pacientes atendidas en el  IAHULA- MERIDA/ VENEZUELA 2014 

X	0	1	2	3
P (X=x)	0,125	0,375	0,375	0,125

Fuente: datos supuestos

F(X)=   0 ≤  X  <0

            0,125 ≤ X <1

            0,5≤ X < 2  

            0,875 ≤ X<3  

Se obtuvo como resultado que la mayor probabilidad de embarazos ectópicos de las mujeres asistentes a la consulta se encuentra entre las edades comprendidas de 21 a 27 años y de 28 años a 33 años, existiendo una probabilidad entre la muestra de mujeres estudiadas de 0,375/8

Propiedades de la Esperanza matemática, varianza y desviación estándar

                   Propiedades de la esperanza matemática

Propiedad de la Esperanza matematica 

1   La esperanza matemática de una constante es igual a esa misma constante, es decir, si c es una constante

E[c] = c.

Ejemplo 1;

X= {2} = E(X)= 2

2  Si las variable X y Y son aleatorias, se cumple:

E(X+Y)= E(X) + E (Y)

Esto indica que el valor de la suma de las dos variables aleatorias es igual a la suma de los dos valores esperados

Ejemplo 2;

Tabla 1. Tabla de probabilidad

X	1	2	3	4
P (X=x)	1/8	3/8	3/8	1/8

E(X)= (1.1/8)+ (2.3/8)+(3.3/8)+(4.1/8)

E(X)= 0,125+0,75+1,125+0,5

E(X)= 2,5

Tabla 2. Tabla de probabilidad de Y

X	1	2
P(Y=y)	2/5	1/3

E (Y)= (1.2/5)+ (2.1/3)

E (Y)= 0,4+0,66=

E (Y)= 1,06

Entonces

E(X+Y)= 2,5+1,06= 3,56 es la esperanza matemática de E(X+Y)

3   El valor esperado del producto de una constante por una variable aleatoria es igual al producto de la constante por el valor esperado de la variable

Entonces:

E (k.X)= k. E(X)

Ejemplo 3:

Dado de k es una constante k=2 y E(X)= 2,5 (valor hallado en el ejemplo 1)

E(k.X) = 2.2,5

E(k.X)= 5

4.    Si las variables X y Y son variables independientes, se cumple que:

E (X.Y)= E(X).E (Y)

Ejemplo 4:

Se utilizaran los valores hallados en el ejemplo 1

E(X.Y)= 2,5 x 1,06

E(X.Y)= 2,65

Propiedades de la varianza y desviación estandar

Cabe destacar que la varianza y la desviación poseen las mismas propiedades, existiendo una variabilidad en el cálculo de la raíz en la desviación al resultado de la varianza

 1 . La varianza de una constante a es cero.

V(K)= 0

Ejemplo:

Dado que X=4 y P(X)= 0,4

V(X)= (4-4)^2. 0,4

V(X)= 0

2.  . Si todos los datos se multiplican por una constante, la varianza queda multiplicada por el cuadrado de la constante.

Entonces:

V (k.X) = K². V(X)

Tabla 3. Tabla de probabilidad de la variable (X)

X	1	2
P(X=x)	1/5	1/8

E(X)= 0,343

Var(X)= (0,343-1)².1/5+ (0,343-2)².1/8

Var(X)= 0,0863+0,3432

Var(X)=0,4295

Dado que k=4

V (k.X) = 4². 0,4295

V (k.X)= 6,872

DE(k.X)= 2,621

3.  . Si las variables X y Y son variables independientes

Var(X+Y)= Var(X)+ Var(Y)

          

    Tabla 4. Tabla de probabilidad de la variable (Y)

X	1	2
P(Y=y)	3/5	2/8

E(X)= 0,343

Var(Y)= (0,343-1)² . 3/5 + (0,343-2)².2/8

Var(Y)= 0,2589+0,6864

Var(Y)=0,9453

Tenemos que:

Var(X)= 0,4295 (ejemplo de la propiedad anterior)

Var(Y)= 0,9453

Var(X+Y)= 0,4295+ 0,9453

Var(X+Y)= 1,3748

DE(X+Y)= 1,725

¿PROBLEMAS DE PROBABILIDAD EN SALUD?

En la actualidad el sistema de salud se ve afectado por las diferentes pandemias erradicadas de un tiempo atrás,  malaria, ebola, el virus de chikunguya son algunas de ellas. El tratamiento de estas patologías se ve ausente producto de la cantidad de pacientes afectados por lo que los medicamentos deben ser distribuidos equitativamente en todos los centros asistenciales u hospitales tipo III que es al lugar donde son  enviados los portadores de estas enfermedades. En esta situación debe ser aplicada la probabilidad ya que se debe tener un aproximado de la cantidad de pacientes portadores,  se debe también tener la previsión del aumento o disminución de la aparición de un ejemplo el virus del chicunguya.

Problema de salud

En el hospital central “José maría Vargas” de san cristobal edo-Tachira, se realiza un estudio de la cantidad de paciente este centro asistencial que posean el virus del chikunguya para así solicitar el tratamiento preventivo para la siguiente semana, mas sin embargo se quiere saber también el sexo de esos pacientes para investigar la incidencia de género y conocer quién es el más afectado por esta pandemia y si son alergicos.  Por ello, se debe realizar un informe para enviar a la corporación de salud (CORPOSALUD) en  solicitud de estos medicamentos pero sin embargo se tiene un límite de 2500 medicamentos entre acetaminofén y analgésicos como paracetamol.

Para la realización de dicho informe es necesario hallar probabilidad, si por ejemplo se sabe semanalmente se diagnostican 20 casos casos en promedio entonces será poco probable que se necesiten más de 50 cajas de acetaminofén y analgesicos para esta enfermedad. Si durante la siguiente semana se incrementa el numero de casos quizá se deba solicitar 10 cajas preventivas de medicamentos para tratar esta enfermedad. En conclusión es necesario hallar un espacio muestral y determinar el número de tratamientos apropiados según el índice de frecuencia de la enfermedad, todo esto en base a los 2500 medicamentos que han dado como tope en corposalud.

En la relación a la incidencia en la afección del sexo de los pacientes que actualmente lo poseen teniendo que 8 son mujeres y 12 son hombres, se calcula que:

a)      Sea mujer

 P(A)=   8             0,4 ES LA PROBABILIDAD DE QUE LOS PACIENTES

             20                  INFECTADOS SEAN DE SEXO     

                                   FEMENINO   

b)      Sea hombre

 P(B)=      12            0,6 ES LA PROBABILIDAD DE QUE LOS PACIENTES

                 20                  INFECTADOS SEAN DE SEXO               

                                       MASCULINO       

La probabilidad, en relación con las ciencias de la salud

Actualmente la estadística es aplicada en todas las áreas de estudio desde saber cuántas personas son oriundas de un estado para compararlo con el total de la población de un país hasta conocer la frecuencia con la que un evento ocurre, en este ultimo podemos compararlo con el área de la salud y su relación con la probabilidad. La probabilidad es medir de forma numérica con qué frecuencia ocurre un evento estudiando todas las variables de ese evento y  si probable o improbable que ocurra, en el area de la salud se emplea este concepto al momento de implementar un tratamiento a determinado paciente dependiendo de su condición es decir, si el paciente acude a una consulta con su especialista por un dolor abdominal y el médico realiza las preguntar pertinentes como “si es alérgico a un medicamento o no, o si lleva un ritmo de vida alterado o si su alimentación es de calidad” y este observa que el paciente es poco sincero al momento del interrogatorio existe la probabilidad de que este mintiendo pero sin embargo el profesional de la salud le receta su debido tratamiento evaluando todos los pro y contras del medicamento que está administrando a su paciente  y de su estilo de vida. También se puede medir dicha frecuencia en el contexto de evaluar los factores de riesgo en las enfermedades y traumatismos analizando las variables que pueden afectar la evolución beneficiosa del paciente buscando resultados y sacando conclusiones  para implementar sistemas que ayuden a disminuir ese factor y su frecuencia.

Así mismo se necesitan veracidad y justificación en la información aplicada para los estudios de los fármacos y las patologías y también en reconocer los síntomas relacionados a determinadas patologías, para encontrar el motivo y el porqué de la sintomatología de los pacientes que asisten a consulta y ayudarles a una pronta mejoría ,esto logra con el empleo de la probabilidad, ya que es un método que permite analizar datos veraces, que se obtienen de un riguroso proceso de estudio-comparativo y así obtener la mejoría y satisfacción de los pacientes